| Question | 98. Validate Binary Search Tree – Leetcode Javascript Solution |
| Difficulty | Medium |
| Question Type | Tree, Binary Tree |
| Question Link | https://leetcode.com/problems/validate-binary-search-tree/ |
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- Both the left and right subtrees must also be binary search trees.
Example 1:

Input: root = [2,1,3]
Output: trueExample 2:
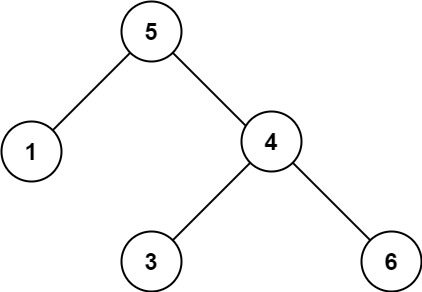
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.Constraints:
The number of nodes in the tree is in the range [1, 104].
-231 <= Node.val <= 231 - 1What is Binary Search Tree?
First of all, we need to understand what is binary search tree.
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.

Solution Logic Decision :
As it is a binary tree, we can start with Breadth First Search(BFS) method to solve. But to validate tree, we need previous root level node on each comparision and traversing by each level, its harder to track root level node value to validate. So, it brings up worst performance on BFS method. So, we can move to DFS approach to solve this.
Solution : (using Depth First Search [DFS] method )
Depth First Search(DFS) is also a traversal approach in which the traverse begins at the root node and proceeds through the nodes as far as possible until we reach the node with no unvisited nearby nodes.
DFS algorithm is a recursive algorithm that uses the idea of backtracking.

Before start coding in to DFS, we first need to decide, which traversal approach we are going to implement solution for the problem.
In DFS we have to decide 3 methods of traversing a tree have a particular order they follow:
- For Inorder, you traverse from the left subtree to the root then to the right subtree.
- For Preorder, you traverse from the root to the left subtree then to the right subtree.
- For Postorder, you traverse from the left subtree to the right subtree then to the root.
Here is a way of representing the information above:

Comparing among 3 traversal order methods, Inorder and Postorder methods will start from Left node of tree. In this case root node comparison becomes inefficient compare to Preorder traversal. In Preorder traversal, we start with root node and compare with left and right nodes. In this case traversal is efficient for this problem. So, we will chose Preorder traversal in DFS to solve this problem. Lets start coding.
Coding Explanation:
Since we decided to go Preorder travesal, from root we need to check on left and right values recursively.
While checking on left node, we need boundaries to compare, so the value will not be below the node value and to chose compare value which is less than node value, we can take lower value of node values. Which we can assume and take value is not lesser than negative infinite value. At the same time on rightmost comparision we can take positive Infinite value to take for comparision.
dfs(root, -Infinity, Infinity);So, in DFS method, we can take min and max values as infinite value initially start with traversal.
When node is left, we update max value as node value and start check whether it satisfy the comparision and then return true or false based on this.
dfs(node.left, min, node.val)At the same time, for right side node, we update min value as node value and start check accordingly.
dfs(node.right, node.val, max)And, if value is lesser than min and greater than max, simply return false because it is not satisfying binary search tree condition of left value is lesser than node and right value greater than node. In this way we can validate given tree is valid or not.
(node.val <= min || node.val >= max)For better understanding, illustrated how value is being compared on each level.

// ------ Depth First Search - Preorder Traversal start - jsdiet.com ------
var isValidBST = function (root) {
if (!root) {
return true;
}
return dfs(root, -Infinity, Infinity);
};
const dfs = (node, min, max) => {
if (node.val <= min || node.val >= max) {
return false;
}
if (node.left) {
if (!dfs(node.left, min, node.val)) {
return false;
}
}
if (node.right) {
if (!dfs(node.right, node.val, max)) {
return false;
}
}
return true;
}
// ------ Depth First Search - Preorder Traversal end - jsdiet.com ------
// Leetcode environment provides already generated binary tree.
// So below part of code no need, if you are trying in Leetcode website environment.
// ------- Code to generate our binary tree -------
// This is purely for testing in local machine
class TreeNode {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
insert(values) {
const queue = [this];
let i = 0;
while (queue.length > 0) {
let current = queue.shift();
for (let side of ["left", "right"]) {
if (!current[side]) {
if (values[i] !== null) {
current[side] = new TreeNode(values[i]);
}
i++;
if (i >= values.length) return this;
}
if (current[side]) queue.push(current[side]);
}
}
return this;
}
}
const tree = new TreeNode(2);
tree.insert([1, 3]);
const tree2 = new TreeNode(5);
tree2.insert([1, 4, null, null, 3, 6]);
// Execute using DFS
let val = isValidBST(tree);
console.log(val);
let val2 = isValidBST(tree2);
console.log(val2);Complexity Analysis :
Time complexity: O(n)
Space complexity: O(H)
Time complexity: O(n), where n is number of nodes in the binary tree.
Space complexity: O(H), where H is Max height of Binary Tree, since we are using DFS approach. Usually, we call as O(n) space complexity because of recursive calls.
DFS is better approach compare to BFS, while traversing among left and right side in depth level.
If you have any doubts, add in comment section. Will clarify at my level best. Also, if you have better solution, kindly share it, will grow together as to become better engineer.


